原题

给你一个 值互不相同 的二叉树的根节点 root 。

在一步操作中，你可以选择 同一层 上任意两个节点，交换这两个节点的值。

返回每一层按 严格递增顺序 排序所需的最少操作数目。

节点的 层数 是该节点和根节点之间的路径的边数。

示例 1 ：

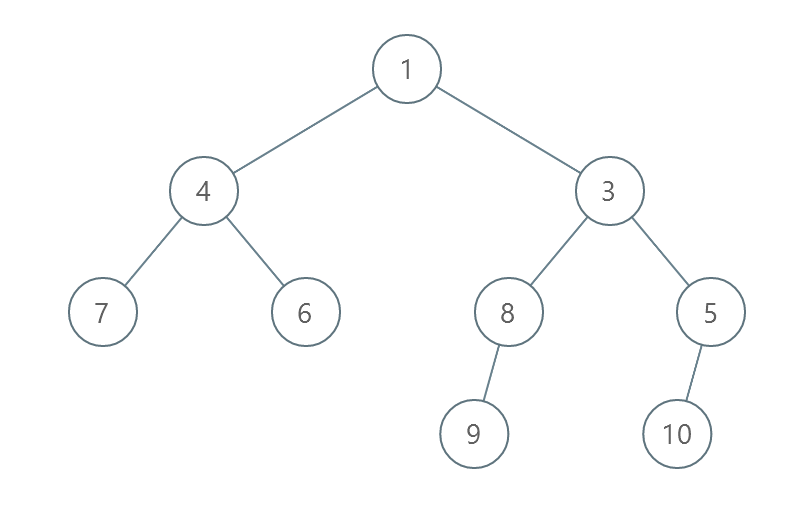
输入：root = [1,4,3,7,6,8,5,null,null,null,null,9,null,10]
输出：3
解释：

• 交换 4 和 3 。第 2 层变为 [3,4] 。
• 交换 7 和 5 。第 3 层变为 [5,6,8,7] 。
• 交换 8 和 7 。第 3 层变为 [5,6,7,8] 。
  共计用了 3 步操作，所以返回 3 。
  可以证明 3 是需要的最少操作数目。

示例 2 ：

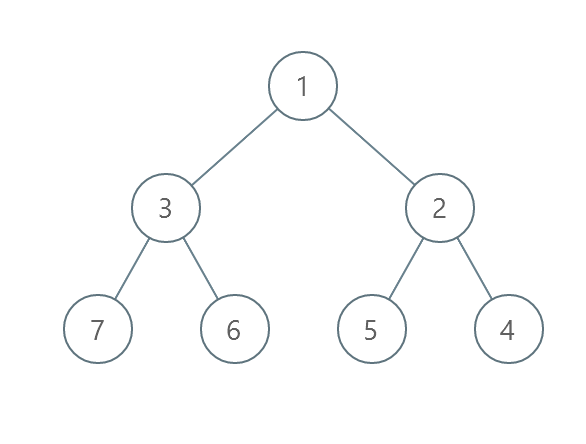
输入：root = [1,3,2,7,6,5,4]
输出：3
解释：

• 交换 3 和 2 。第 2 层变为 [2,3] 。
• 交换 7 和 4 。第 3 层变为 [4,6,5,7] 。
• 交换 6 和 5 。第 3 层变为 [4,5,6,7] 。
  共计用了 3 步操作，所以返回 3 。
  可以证明 3 是需要的最少操作数目。

示例 3 ：

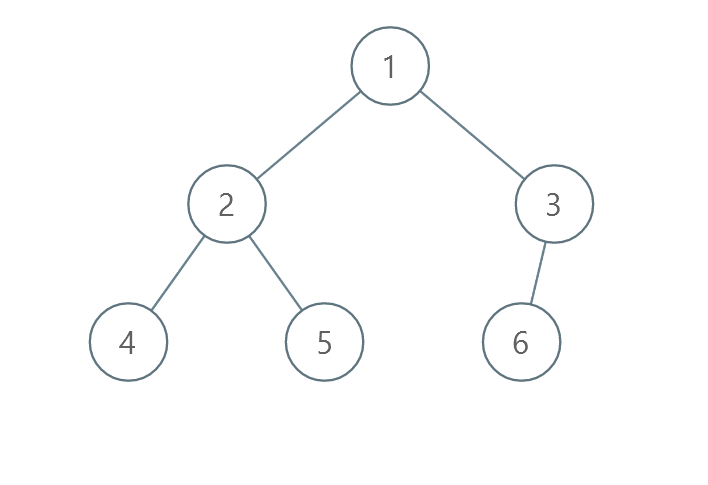
输入：root = [1,2,3,4,5,6]
输出：0
解释：每一层已经按递增顺序排序，所以返回 0。

提示：

• 树中节点的数目在范围 [1, 10^5] 。
• 1 <= Node.val <= 10^5
• 树中的所有值 互不相同 。

思路

题目要我们将每层的数据排序并找到最少交换次数，很显然，我们可以用二叉树的层序遍历将数据取出来，层序遍历可以使用BFS的思路实现。这里就不多赘述。

但是如何获得最少交换次数呢？
这就需要置换环了，我们可以数据排序前的下标使用一个map保存下来，将数据排序，将其与排序前的位置对比，如果对比到的数据不同，那么代表该数据发生了交换，我们可以沿着数据一路寻找下去，最后会找到自身，成为一个环，那么这个环就是置换环，环内数据依次交换，该环交换次数即得n - 1，找出数组所有的环，将其相加，即可获得总最少交换次数，为数据数据数 - 环数。

用这个思路去结合BFS，即可求得结果。

代码

• leetcode AC片段：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minimumOperations(TreeNode* root) {
        int ans = 0;
        map<int, int> m; // 检测环
        queue<TreeNode *> q; // bfs
        map<TreeNode*, int> c; // 层数

        q.push(root);
        c[root] = 1;
        int nowC = 1;
        while (!q.empty()) {
            m.clear();
            int cnt = 0;
            vector<int> before;
            while (c[q.front()] == nowC) {
                TreeNode* nowNode = q.front();
                q.pop();
                before.push_back(nowNode->val);
                m[nowNode->val] = cnt++;
                if (nowNode->left != nullptr) {
                    q.push(nowNode->left);
                    c[nowNode->left] = nowC + 1;
                }
                if (nowNode->right != nullptr) {
                    q.push(nowNode->right);
                    c[nowNode->right] = nowC + 1;
                }
            }
            if (!q.empty()) nowC = c[q.front()];

            vector<int> after(before);
            sort(after.begin(), after.end());

            vector<bool> flag(after.size());
            int loop = 0;
            for(int i = 0; i < after.size(); i++) {
                int index = i, num = after[i];
                if (!flag[index]) { // 未加入环的情况
                    while (!flag[index]) {
                        flag[index] = true;
                        index = m[num];
                        num = after[index];
                    }
                    loop += 1;
                }
            }
            ans += after.size() - loop;
        }

        return ans;
    }
};

• 为方便本地调试，写了个本地调试片段（建树），用-1代表了null

#include <bits/stdc++.h>
using namespace std;

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
class Solution {
public:
    int minimumOperations(TreeNode* root) {
        int ans = 0;
        map<int, int> m; // 检测环
        queue<TreeNode *> q; // bfs
        map<TreeNode*, int> c; // 层数

        q.push(root);
        c[root] = 1;
        int nowC = 1;
        while (!q.empty()) {
            m.clear();
            int cnt = 0;
            vector<int> before;
            while (c[q.front()] == nowC) {
                TreeNode* nowNode = q.front();
                q.pop();
                before.push_back(nowNode->val);
                m[nowNode->val] = cnt++;
                if (nowNode->left != nullptr) {
                    q.push(nowNode->left);
                    c[nowNode->left] = nowC + 1;
                }
                if (nowNode->right != nullptr) {
                    q.push(nowNode->right);
                    c[nowNode->right] = nowC + 1;
                }
            }
            if (!q.empty()) nowC = c[q.front()];

            vector<int> after(before);
            sort(after.begin(), after.end());

            vector<bool> flag(after.size());
            int loop = 0;
            for(int i = 0; i < after.size(); i++) {
                int index = i, num = after[i];
                if (!flag[index]) { // 未加入环的情况
                    while (!flag[index]) {
                        flag[index] = true;
                        index = m[num];
                        num = after[index];
                    }
                    loop += 1;
                }
            }
            ans += after.size() - loop;
        }

        return ans;
    }
};
TreeNode* init(vector<int> nums) {
    map<TreeNode*, bool> l, r;
    queue<TreeNode*> q;
    TreeNode* nowNode = nullptr, *root = nullptr;
    for (auto i : nums) {

        if (q.empty()) {
            auto temp = new TreeNode(i);
            root = nowNode = temp;
            q.push(nowNode);
        } else {
            if (nowNode->left == nullptr && !l[nowNode]) {
                if (i == -1) {
                    l[nowNode] = true;
                } else {
                    nowNode->left = new TreeNode(i);
                    q.push(nowNode->left);
                }
            } else if (nowNode->right == nullptr && !r[nowNode]) {
                if (i == -1) r[nowNode] = true;
                else {
                    nowNode->right = new TreeNode(i);
                    q.push(nowNode->right);
                }
                q.pop();
                nowNode = q.front();
            }
        }
    }
    return root;
}
int main() {
    Solution s;

    vector<int> c({1,4,3,7,6,8,5,-1,-1,-1,-1,9,-1,10});
    cout << s.minimumOperations(init(c));
    return 0;
}